微软Mathematics数学工具

微软Mathematics提供了一系列数学工具，可帮助学生快速轻松地完成作业。有了 Microsoft Mathematics，学生们可以逐步学习解方程，同时能更好地理解初等代数、代数、三角、物理、化学和微积分中的基本概念。

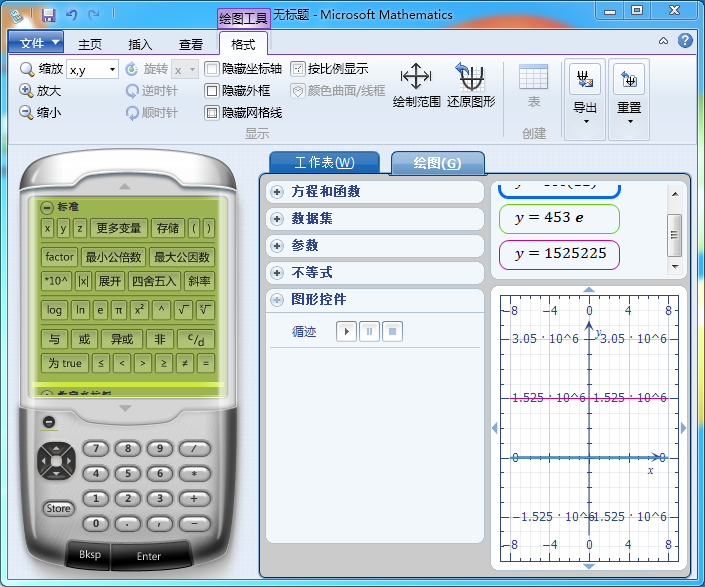
Microsoft Mathematics包括一个功能全面的绘图计算器，该计算器被设计为能像手持计算器一样工作。

Microsoft Mathematics 还有其他数学工具，可帮助您计算三角函数、从一种单位制转换成另一种单位制以及解方程组。

功能特点：

1. 计算标准数学函数变量之间的数学关系。

在此关系中，一个变量的值可确定另一个变量的唯一值，如求根和对数为得到给定数字而必须对底数采用的幂。

解方程一个数学语句，通常是用等号分隔的两个表达式，它们的值相等和不等式。
2. 解三角形。

从一种度量单位转换成另一个度量单位。

计算三角函数，如正弦一个三角函数，对于直角三角形中的给定角，该函数等于该角的对边长度除以斜边和余弦一个三角函数。

对于直角三角形中的一个给定角，该函数等于该角所对的邻边长度除以斜边。

3. 执行矩阵数学元素的矩形数组。

例如线性方程的系数，其行和列可与其他数组的行和列组合在一起求解问题和向量具有大小和方向的数量。

向量的示例包括力和速度操作，如求逆和叉积。

4. 计算基本统计信息。

如平均数集合中所有元素的和除以集合中的元素数得到的值。

也称为算术平均数或均值。和标准差一种数量的统计信息度量，表示一组值相对于算术平均值的偏差，它等于差值平方的平均值的平方根。

进行复数一个形式为 a + bi 的数字，其中，a 和 b 是实数，i = sqrt(-1)，因此 bi 是虚数，除非 b = 0运算。

其他说明：

在笛卡尔坐标系提 供平面上某点的位置的一对坐标（相对于原点和两个互相垂直的轴）。

或者提供空间上某点的位置的三个坐标的组合（相对于原点和三个互相垂直的平面）。

极坐标系通过指定向量径的长度及其与水平线形成的角度在平面中为点定位的一对坐标、柱坐标系和球用于在空间中为点定位的一组坐标。

以相对于某个原点的距离和描述 其相对于自该原点展开的垂直轴的方向的角度表示坐标系中绘制二维图形和三维图形。

计算级数带有下标的项的和（可能无穷大）。的导数一个从其他函数导出的函数。

这种情况下，在原函数的每个点上，导数都表示原函数在该点的斜率。

积分也称 为反导数，函数的不定积分是将原函数作为其导数的函数。

极限当给定函数的自变量的所有值充分接近但不等于给定数（或者无穷大的正数或负数）时任意接近于 该函数的值的数。